Moon Phase formula - updated

[p.hennessey]

Would you consider recalculating both your simple and complex moon phase formulas using a more robust source?

https://giangrandi.org/soft/mooncalc/mooncalc.shtml

If you view the page source (and scroll down in the code to the <script> section to find the array titled moon_phases_list) you’ll see 100 years of moon data (!) that is calculated using highly accurate methods. Might be fun to use this data as your basis, see how close your formulas are…and then outdo yourself once again!

Worth a shot? If you do this, you’ll probably have the most accurate closed-form moon phase formula on the entire web.

[mikeoday]

Thanks for the link and the suggestion. I will take a look. Cheers.

[mikeoday]

Mmm, not sure that there will be much to be gained. The list they have is for four phases and comes from NASA. The data I used has four phases and comes from the US Navy Observatory which is the official source ( NASA is not the official source ). The times might be different but there is no way of knowing which prediction is more likely to be correct. Indeed, the way one would normally check such data is to compare it to the US Navy data ( as the official true data ). What would be good would be to have data for more than the four phases to fill in the gaps in the US Navy data - assuming that the 4 phases in the more detailed set still align with the US Navy data.

Thanks again.

Cheers
Mike

[p.hennessey]

Your equations did not take into account the longer 100-year timeline — the additional data should allow you to adjust your parameters so that the error is minimized over a longer period of time. AFAIK the methods used in the calculations of this lunar data are as good as what the US Navy Observatory uses (at least for this purpose).

I attempted to analyze your equation parameters against the data and, as you can see in the attached screenshot, your settings provide very low error rates in the 20-year span you corrected for — but then it starts to deviate quite a bit before and after that point.

I normalized the field as integers (in a section of the table not shown in this screenshot) so that I could play with the values easily, but I do not know how to modify the parameters to reduce the error over the entire 100-year period.

Hoping you’re still up for the challenge! I could send you this excel document if that would be helpful.

[hippocampus.watches]

Wow ladies and gentlemens, i proudly presents… experts at work

[p.hennessey]

Ladies and gentlemen… I did it!

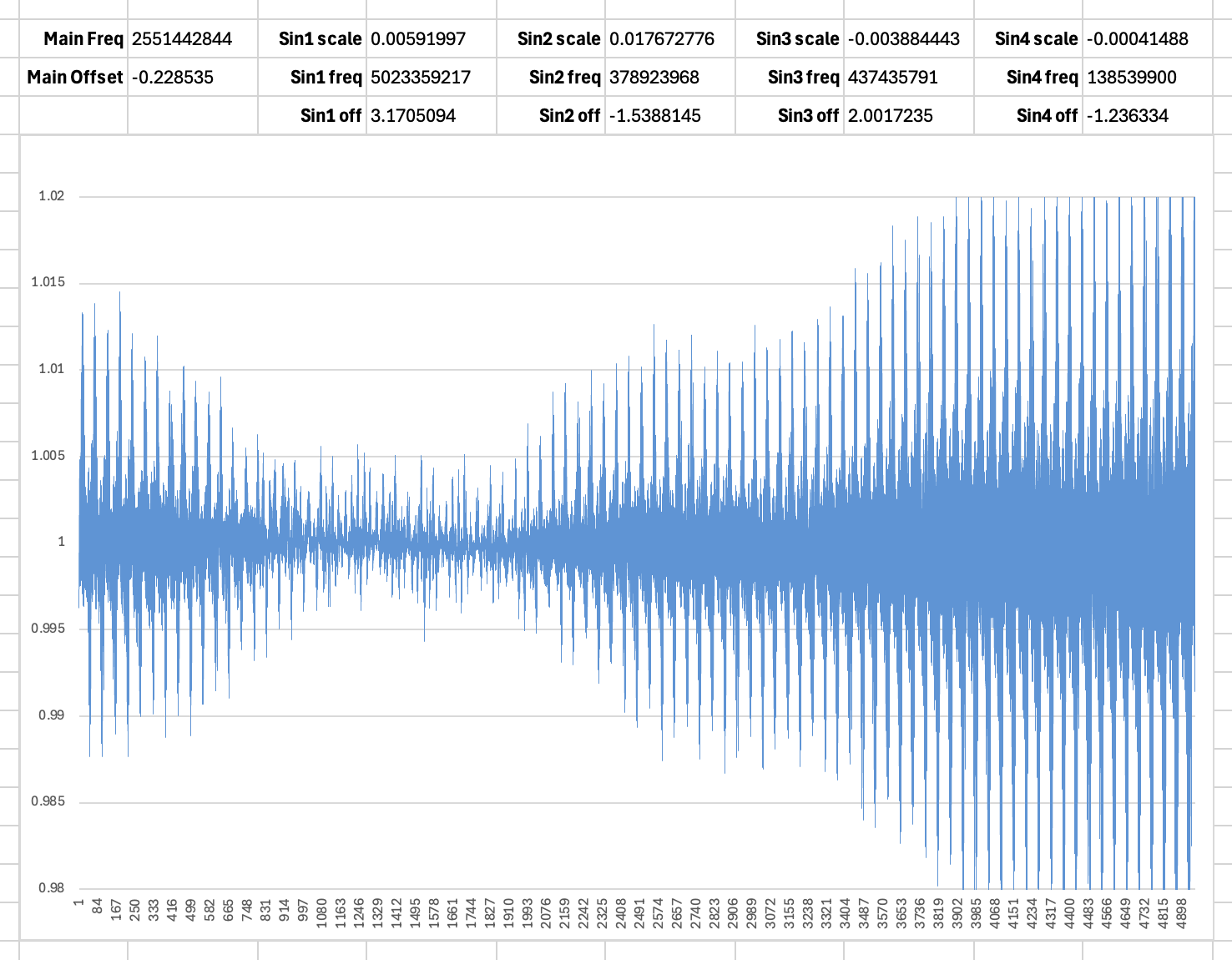
I used Fourier analysis and Discrete Fourier Transforms to reverse-engineer the next 75 years of moon phase data. This allowed me to derive a new phase equation that is very compact, extremely accurate, and will remain so for… probably the next 1000 years.

This was a long and arduous process. I had to learn some python code and I used Chat GPT to help me learn these unfamiliar concepts, which was essential in helping me fit a new series of sin curves to the moon data.

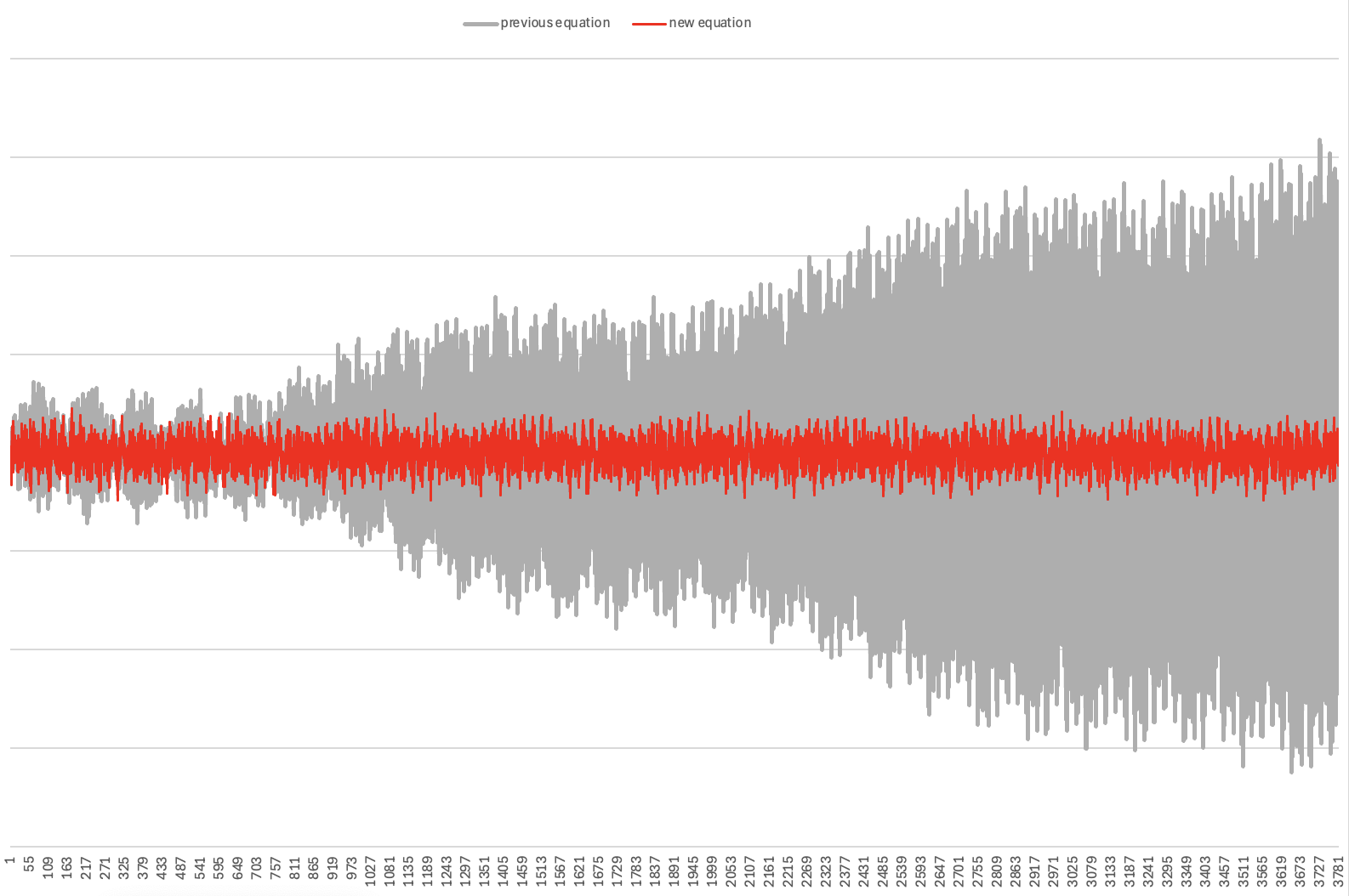
Here is a comparison between the relative error of @mikeoday’s previous equation (which really is very accurate) and mine (shown in red) from today’s date until the year 2100. You can see that Mike’s equation is pretty stable for the next 20 years or so, but then it starts to become more inaccurate over time.

Here are the equations formatted for both Facer and for Python in case some of you want to run it through your own paces:

(((#DNOW#/2551442844-0.228535)
+0.01765sin(#DNOW#/378902233-1.828)
+0.00583sin(#DNOW#/5022682843-3.179)
-0.00383sin(#DNOW#/437445587-4.186)
-0.00057sin(#DNOW#/218722742-2.084))%1)

Here’s a 1-line version that is easy to copy into Facer Creator:

(((#DNOW#/2551442844-0.228535)+0.01765sin(#DNOW#/378902233-1.828)+0.00583sin(#DNOW#/5022682843-3.179)-0.00383sin(#DNOW#/437445587-4.186)-0.00057sin(#DNOW#/218722742-2.084))%1)

Here’s a version that works in Python, which uses Unix time output in seconds (instead of milliseconds like Facer’s “#DNOW#” function does) so we have to adjust our scalars in the formula slightly:

import time
import math

def moonPhaseCalc():
    cTime = time.time()
    mCalc = ( ( cTime / 2551442.844 - 0.228535 )
    + 0.01765 * math.sin( cTime /  378902.233 - 1.828 )
    + 0.00583 * math.sin( cTime / 5022682.843 - 3.179 )
    - 0.00383 * math.sin( cTime /  437445.587 - 4.186 )
    - 0.00057 * math.sin( cTime /  218722.742 - 2.084 ) )
    return mCalc % 1

print(moonPhaseCalc())

Now… could I make it even more accurate? …Perhaps, but we’re at a point of diminishing returns here. My new equation should be no more than 20 minutes off from the true phase of the moon, and for all practical purposes… this is probably overkill.

That being said, I couldn’t resist the challenge. And frankly, I hope someone else attempts to improve on it! Many thanks to @mikeoday for the original formulation, which was highly instructive and gave me a great starting point — all I’ve done is derive new values for the other terms. I may post again with further refinements, but this is pretty good now!

Cheers!

[russellcresser]

WOW. I used @mikeoday Formula for my moon age stuff. Always with Thanks. Since Facer Launched #MOONAGEPERCENT# I have been using that. The way I have been using it ( crudly ) it is within half a day of my other moon Data I use. I am wondering how it stacks up to the work you have done. I can not pretend to do the work you have done. I am from the school of Copy and Paste. Thank you very much Indeed for your work. I often say that Science can not be done on our Watches. I was wrong to say that.
.
@p.hennessey Sadly your reworked formula will not work for me in creator and I am not clever enough o fix it . I think it needs to be on one line and format protected . I guess some formatting has crept in and it shows nothing . I look forward to testing it .

OK I fixed it . The * went missing . As they often do . Thankfully the strategy is the same as Mikes so I was able to spot the difference .
.

(((#DNOW#/2551442844-0.228535)+0.01765*sin(#DNOW#/378902233-1.828)+0.00583*sin(#DNOW#/5022682843-3.179)-0.00383*sin(#DNOW#/437445587-4.186)-0.00057*sin(#DNOW#/218722742-2.084))%1)

.

Tests Follow .

[russellcresser]

I would like to thank you Guys and Everyone that contributes to this Amazing Community .

Someone on the WFS Forum is asking where he might find resources like Hands and Dials . Not only those but also these contributions of Formulas that can Elevate work done on Face to the Upper Level are amazing . Totally Unique and Totally amazing . I am actually very Proud to call myself part of this community .
Under test I find the difference between the two Complex formulas in the year 2100 two minutes or there about . If my memory serves me the Unix Epoch Timer ( #DNOW# ) will be redundant by that time . Roll on the 64 Bit one which as far as I know has not been named yet . I kind of guess they will just patch the 64 bit count in one day in 2038 I believe

.

.

[p.hennessey]

Please bear in mind that the data I used to derive this updated formula came from the work of Fred Espenak (NASA/GSFC).

Moon Phases: 2001 to 2100 GMT

It should be noted that Fred is responsible for calculating NASA’s solar eclipse maps:
https://www.researchgate.net/figure/Eclipse-Predictions-by-Fred-Espenak-NASAs-GSFC-http-eclipsegsfcnasagov-Figure_fig2_380630045

[russellcresser]

Yes . I know that NASA is considered one of the standards and the US Navy Data . Did you get time to check the Facer Tag .

[p.hennessey]

I’m not sure what a Facer tag is… I must confess that I am not a user of Facer. I am an astronomy enthusiast and recreational programmer, and I found this message thread after trying to research my own moon phase formula.

Edit: This site has rules for new users that prevents me from replying further (I am only able to update previous posts.) I think that I might start a new thread that is dedicated to the moon phase calculation and cataloging the progress made in this thread.

Quick note: I compared the NASA data with the NAVY data, and they are identical most of the time, and only differ by a maximum of 2 minutes at any given moment. My formula works well with either data set (as does Mike’s).

[russellcresser]

Ok . Well I think your contribution is appreciated . The facer TAG is an element in Facer Creator that gives the age of the Moon 0 to 1 beginning at the New Moon . #MOONAGEPERCENT# . I think you should have a look at the creator Tags they have distance from the earth to the Moons Apogee and some other stuff that I would never use .

[mikeoday]

Congratulations, excellent job!

As for further improvements … you could take a look at the next largest coefficients in your Fourier series to see if they are significant compared to the lowest you currently have ( -0.00057 ). That would give you an indication if it is worth the effort adding more terms.

Thanks for sharing your work and the new “go to standard” for accurate phase predictions!

[mikeoday]

The main issue with the Tag is ( was ? ) that it seems to use local time rather than GMT. That means that the small error that you demonstrate is dwarfed by the timezone difference. So if one lives in the UK, the error won’t be too bad but the further you get from GMT, the larger the error. From memory the maximum timezone difference is of the order of 14hrs. Here it 9 hrs or so. Having said all that, it may have been fixed - I have not checked since shortly after the tags came out. If I get the chance I will take a look - easy enough to do, one just needs to change the timezone on the phone/watch, if it has been fixed the phase will not change.

[mikeoday]

Confirmed - Moon Age tag uses local time not UTC

Phone/Watch set to UTC: age of moon 26.753

Phone/Watch set to local time ( +9.5hrs ): age of moon 27.149

Additional error for my location: 9.5 hours ( ie. timezone offset )

[mikeoday]

I believe the following will correct the #MOONAGE# tag:

((#MOONAGE#+(#DOFST#/1440)+29.530588)%29.530588)

One is still left with any residual small offset that may be there due to the model accessed by the tag but the timezone offset error should be corrected.

edit:

See the following for more details:

#MOONAGE# tag - time zone error

If anyone is using the #MOONAGE# tag and wants to correct the time zone error, I think the following should work: Replace #MOONAGE# with ((#MOONAGE#+(#DOFST#/1440)+29.530588)%29.530588) { Notes: #MOONAGE# returns different values depending on the time zone of the user. The phase of the Moon however is the same for everyone everywhere at the same time, hence the need for the correction. Depending on where one lives the error could by up to 14hrs or so. For example, a person in …

[russellcresser]

Amazing . Thanks Mike . Sadly I have been posting Topics Bigging up the Facer Tag . I have been working in Blissful Ignorance as I am on BST / GMT . I have a gadget on My watch and a few I have published that has the Moon on a stick relative to a 24 Hrs Sun on a stick . Where I am for me it successfully predicts the New Moon the Quarters and Full . Not to mention the Tides . For me it is the Visual aspect of what we see of the Moon in the Sky and it’s approximate position that I am looking for on my Watch so that is good for me . Thanks for this Fantastic work . Everyday must be a Learning Day .

[hippocampus.watches]

wow again one of your legendary test faces

[russellcresser]

@mikeoday or @p.hennessey Please Help if you have some spare Time. In my Ignorance I have been fooling myself that this formula gives me the Moon Illumination Percent Value . While it is right for the Full , New and Quarters it is obviously wrong compared to proper values in-between . Is it possible to get it a bit better with Sin or Cos . Thanking you in anticipation .

(round(100-((abs((#MOONAGEPERCENT#)-0.5))*200)))

[russellcresser]

OK @mikeoday @p.hennessey and @kirium0212 I think I have it . I am Very pleased with myself . This stuff is difficult by trial and error . However thank you all so very much for the Inspiration.
.
.

(50+((sin(rad((((#MOONAGEPERCENT#)*360))-90)))*50))