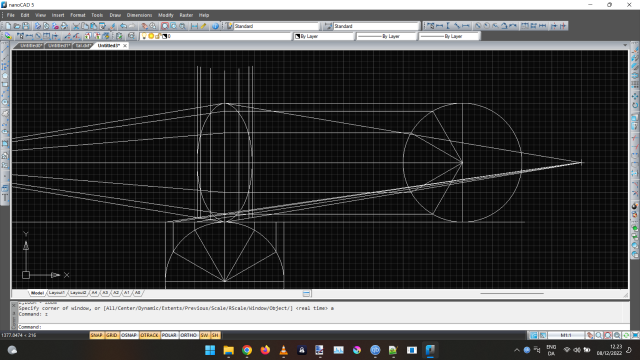
I’ve had a semester of technical drawing where we learned a few things some might find useful when drawing 3d renditions. Most people can eyeball these things, but some, like me, need to draw it up in a more precise way.
I use nanoCAD, which is freeware. It has some annoying glitches, but all in all it is great for simple 2d drawing.
First example is the well known perspective of a block seen looking directly at a corner.
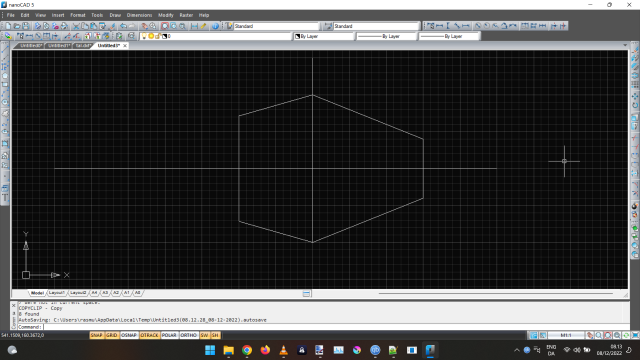
I’ve made it a bit off center and asymmetrical to illustrate things better.
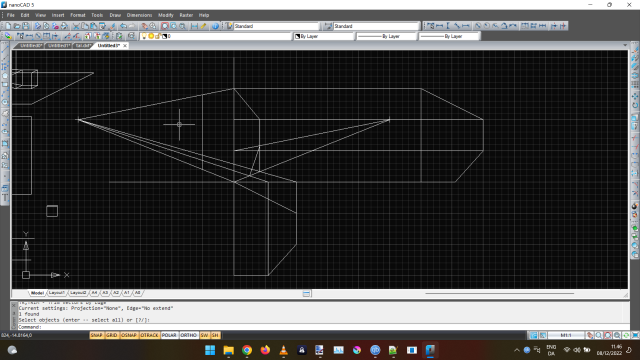
The way to make sure things are in scale, you choose a point to measure from, typically the corner closest to you, the center line in my example. Here the center line is 4 5x5 blocks high.
To measure a distance disappearing into the left, I use a base line, and measure along with that. In the example, I’ve measured 4 blocks down. I then draw a line from the far right point, the “point of disappearing”. Where this line crosses my line from the left is where a point will be equal to the height of the block.
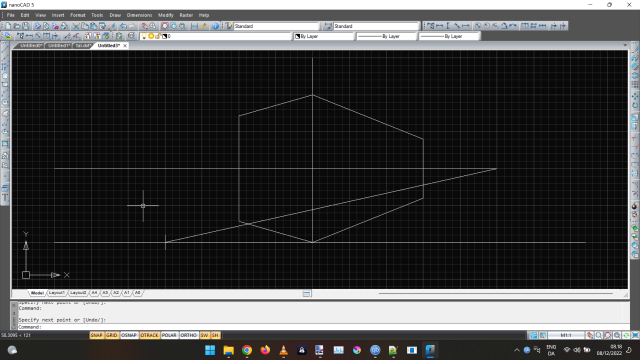
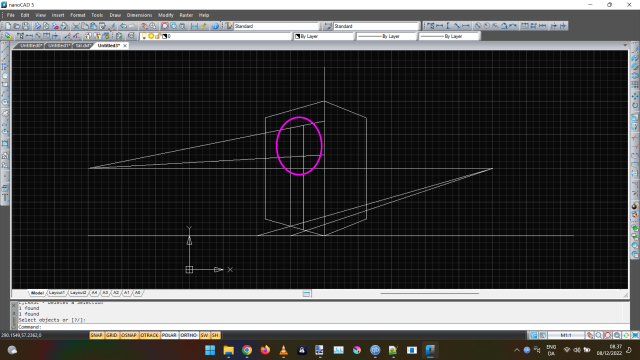
If I do this for both sides, I’ll get this perspective rendition of a cube. On the picture, I’ve circled the intersections.
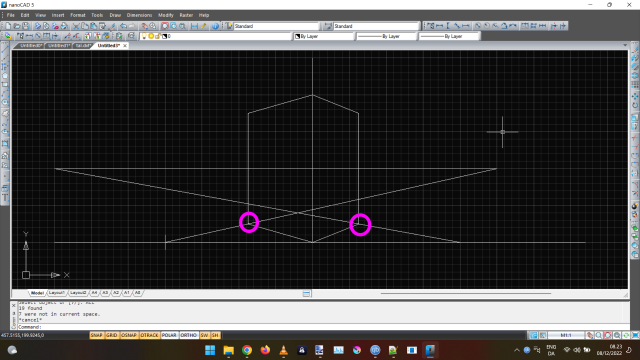
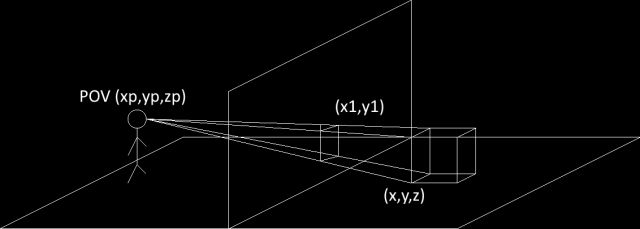
This is an idea of what it would look like from above with the line of sight drawn in. Not a precise picture of it though.
To measure vertically is easy, simply mark the point on the center line and draw the perspective lines. In the picture I’ve drawn a “window” 1x1 blocks, circled in pink.