Hi!
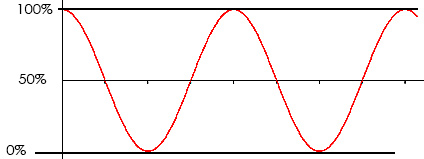
Letting the transparency go out of bounds is probably the easiest way to do this since transparency clips nicely (it can never go higher than 100 or lower than 0). However, if you apply it to something else (like rotation) it won’t work as well. If the rotation has a lowest value of -90 and a highest value of 90 it will oscillate half a lap between the nine position and the three position. If you instead have 0 as lowest and 720 as the highest it will travel two laps from 12 to 12 in one direction, then two laps back again.
In order to make this work in a more general way we could use the clamp() function to limit the values. clamp() lets you define an input value, a lowest value and a highest value. If the input value is lower than the defined lowest, it will be stick to that defined lowest. The same in the other direction for the defined highest.
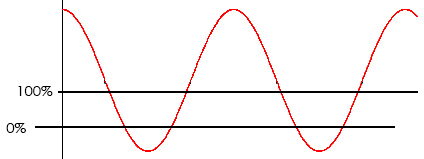
Basically, it would behave exactly like your second graph. Let’s look at an example.
(cos(#DWFSS#/11.5)*180)
This outputs a value from -180 to 180 to -180 again. It moves slower near the extremes, but never really stops. But maybe we want it to go from 0 to 120 instead, spending half its time at 0 and a smaller amount of time at 120. We could then do this:
(clamp((cos(#DWFSS#/11.5)*180),0,120))
Right now it spends half its time at 0 since 0 is halway between -180 and 180. In order to make it spend half its time at 120 we need to put the halfway point at 120. We can do this by adding 120 to the sine:
((cos(#DWFSS#/11.5)*180)+120)
And with the clamp:
(clamp(((cos(#DWFSS#/11.5)*180)+120),0,120))
In a general way, this is how the formula works:
(clamp(((cos(RATE)*HEIGHT)+POSITION),MIN,MAX))
To make it work like in the second graph, we use 0 and 100 as our MIN and MAX. The sine seems to be about four times larger than the distance between 0 and 100 so for HEIGHT we’ll use 200 since it will make it go between -200 and 200. The midpoint of the sine seems to be at about 125 so that’s our POSITION. Finally, for our rate I’ll just use the same provided in the third post. This gives us the following:
(clamp(((cos(#DWFSS#/11.5)*200)+125),0,100))
The final times I get by trying this out aren’t the ones specified in the post, but the concept works out well. By tweaking the values you can get it exactly to where you want it. This works well for any value you want to change, not just transparency, so you can have something move in sync with the transparency if you want.
Hope this helps.


 It works great, but the fade in is a little bit to fast. What value should i change to make it a little bit longer?
It works great, but the fade in is a little bit to fast. What value should i change to make it a little bit longer?