There are a number of triaxial Facer watch faces available, and they are quite unique (links further below). But I have not come across a triaxial watch face where the dials rotate as well. Do post if you know of such jewels!
Inspired by @russellcresser’s picture, I had to take on the challenge:
This is the result:

The face is made up of the following parts:
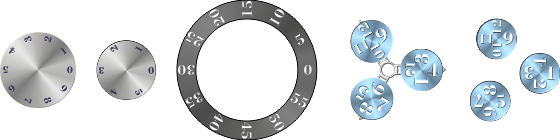
10 Second disk (or last digit of the seconds):
This disk rotates at: ((#DWFSS#*6)+60)
6x as fast as the normal speed of a seconds had (should be logical…). The +60 is the offset, so that the seconds can be read at around 5 o’clock.
1st digit of seconds disk:
The disk should stand still and only rotate when the 9th second approaches. So the disk rotates every 10 seconds, for 60 degrees:
$(#Ds#%10)=9?((floor(#Ds#/10)*60)+60)+(clamp(((((#DWFSS#/6)%60)-#Ds#)*60),0,60)):((floor(#Ds#/10)*60)+60)$
Explanation: if 60 seconds (Ds) are divisible by 10 and the remainder is 9, then rotate from current position (floor…) +60° (+clamp…). And in all other cases, stay where you are (:floor…)
The minutes:
This one is straight forward, rotates as a normal smooth minute hand: #DWFMS#
The rotor:
I must confess, I did not manage without the rotor. The idea was to have the 3 disks for the hours rotate in an orbit, but I did not find a way to change X and Y position for only 120° at a certain point in time. So the rotor becomes active every 4 hours, rotates 120° and then the single disk, positioned at 3 o’clock are overlayed using opacity.
The rotor rotates at 1, 5, and 9 of the value #Dh# (1-12). So, for example, when the time is 12:59:59 and it is going to be 1:00:00, the rotor rotates by 120 degrees to put the 1-4 hour disk into position. Since #Dh# is only a full hour value I add a second condition using the minutes=0 to initiate the rotation:
´$#Dh#=1&&#DWFMS#/6=0?`
Rotation is: (120-(clamp(((((#DWFSS#/6)%60)-#Ds#)*120),0,120)))
Explanation: current position (120) - max 120°
The speed of the rotation always starts at 0, hence subtracting #Ds#
Putting all that into one expression for the 1, 5, and 9:
$#Dh#=1&&#DWFMS#/6=0?(120-(clamp(((((#DWFSS#/6)%60)-#Ds#)*120),0,120))):$$#Dh#=5&&#DWFMS#/6=0?(0-(clamp(((((#DWFSS#/6)%60)-#Ds#)*120),0,120))):$$#Dh#=9&&#DWFMS#/6=0?(240-(clamp(((((#DWFSS#/6)%60)-#Ds#)*120),0,120))):(480-ceil(#Dh#/4)*120)$
For all other values, the rotor should stay in position, so: (480-ceil(#Dh#/4)*120)
The formula gives the value 0, 120, and 240, depending on current hour.
The 3-hour disks
The disks
- stay in position at 3 o’clock,
- are visible at respective hours,
- rotate at the hour
Challenges:
- rotation at hours 1, 5, and 9 should be delayed, since the rotor needs to finish rotating
- 100% opacity should also only be true when the rotor stops
- Each opacity will differ depending on the hour, and should be valid for 4 values. Example for the duration from 1 to 4
Opacity:
Disk 1-4h: $(ceil((#Dh#)/4))=1&&(#DWFMS#+#DK#)>1?100:0$
Disk 5-8h: $(ceil((#Dh#)/4))=2&&(#DWFMS#+#DK#)>5?100:0$
Disk 9-12h: $(ceil((#Dh#)/4))=3&&(#DWFMS#+#Dh#)>9?100:0$
Explanation:
(ceil((#Dh#)/4)) will always be 1, for Dh 1, 2, 3, and 4
The second condition makes sure the 100% opacity kicks in when #DK# (0-1) is greater than 1. If ´#DK#` is not added to the smooth minute value, opacity is “0” every hour for a split second.
Rotation of the hour disks:
The disk rotation is made up of 3 parts:
- a delayed rotation at the hour 1, 5, and 9
- normal rotation at the hour
- stationery value other wise
Example for disk 1-4hour:
$#Dh#=1&&(toFixed(#DWFMS#/6,3))=0.017?(90-(clamp(((((#DWFSS#/6)%60)-#Ds#)*90),0,90))):$$#Dh#=2&&#DWFMS#/6=0?(360-(clamp(((((#DWFSS#/6)%60)-#Ds#)*90),0,90))):$$#Dh#=3&&#DWFMS#/6=0?(270-(clamp(((((#DWFSS#/6)%60)-#Ds#)*90),0,90))):$$#Dh#=4&&#DWFMS#/6=0?(180-(clamp(((((#DWFSS#/6)%60)-#Ds#)*90),0,90))):(450-ceil(#Dh#%4)*90)$
Explanation:
- The delayed rotation is done using the “toFixed” function to give an exact value a little later than at the exact minute value of 0. In this case 0.017 (trial and error value).
- the formula after the “?” is the usual rotation, in this case by 90°, always at a starting position
- the last expression is the value at which the disk should stay put
The other 2 disk rotation formulas are the same, but using 5-8 and 9-12.
