A unique second wheel, where the ones digit of the seconds are always up/down and orbits the tens digit of the seconds, which in turn orbits the centre of the watch face. This is not an image dial which simply rotates, but rather mathematical expressions. Digital zoom is incorporated on the current the second ones digit.
Time, date, current weather condition, current temperature and steps actively change position every 1/4 rotation of the seconds wheel, in order to not overlap any data.
Battery level meter is at the bottom. Green above 60%, red below 30%, and yellow in between.
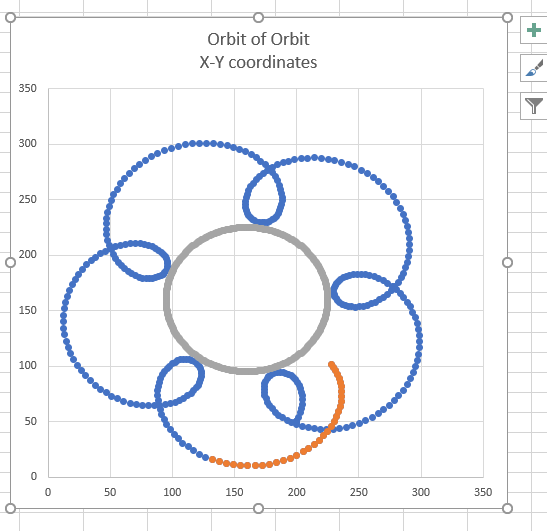
For my fellow watch face designers, you may be interested in the orbital expressions for the numbers in the seconds wheel. It is quite challenging since the orbital sine / cosine equations seem to break down when embedded in the second orbit of the first orbit. I graphed out an X-Y coordinate graph below vs DWFSS value, and the results ended up quite interesting.
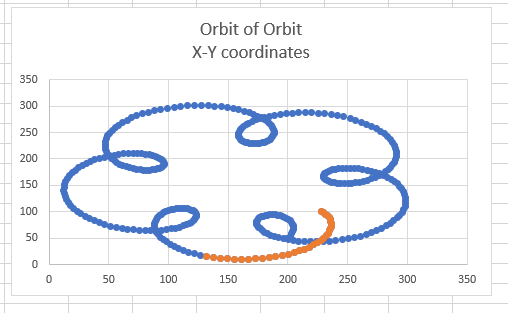
The blue points represent DWFSS values from 0 to 360. The red points represent DWFSS values from 361 to 394.
For the blue points, 0 to 360 no longer represents a full circular motion around the centre point. Rather it has the funny loops and stops short, about 90% of a full circle. You have to extend the DWFSS values beyond 360 in order to evenly distribute, in this case, all 10 digits of the ones seconds digit value. Also, the extension is not linear, as one has to account for the little loops & such. If you actually follow the motion of one particular number, you can see it making the loops per the graph. Also, the embedded expressions do not output the numbers sequentially. Really wild results occurred…
It actually turns out that in my final resultant seconds wheel spin, the wheel should spin 3.5% faster than it really does, so there is a little skip at the transition from the 59 to 60 second mark. But it is hardly noticable unless you are looking for it. I’m really at a loss of how to speed up the second wheel spin by 3.5%, so I just let it slide.
Below are sample expressions for the number 0 of the ones second digit.
X: ((160+cos((#DWFSS#-90)*((pi)/180))*110) + cos((#DWFSS#-0)/10)40)
Y: ((160+sin((#DWFSS#-90)((pi)/180))*110) + sin((#DWFSS#-0)/10)*40)
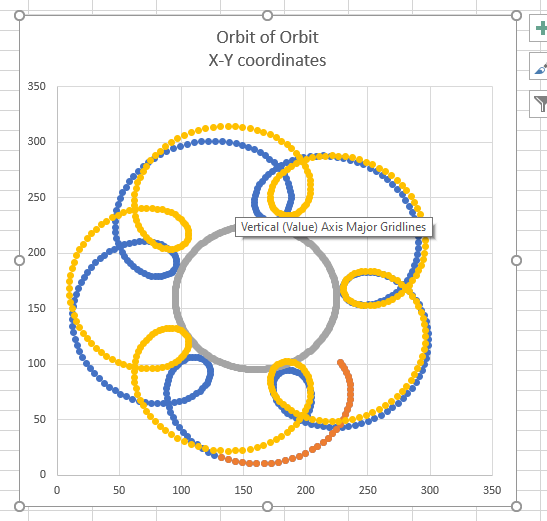
When I graph your expression, it generates a smooth circular motion, as per the grey data series below (they are so close they look like a continuous line):
