Trying to understand ((sin(#DWE#*2)*40)+50)

Watchface Design Expression Help
1

So this string was in the documentation for the breathing effect.
((sin(#DWE#*2)*40)+50)
Iā€™m trying to understand why it does what it does. I think part of my problem is I donā€™t understand sin. I played with the values but couldnā€™t get it to do what I needed it to do. Itā€™s close but just not quite. If I understood what each part of the string did I feel like I could solve my problem.
Thanks,
Orakix

2

Sin is a function that allows you to interpret the length of a side of a right triangle given the length of one side of the triangle, the hypotenuse, and the angle at which those two meet. sin(a)=x / h, where x is the side opposite from the angle, (cos(a)=y / h, where y is the side adjacent to the angle). Its most used in our situation because it provides cycles of motion, because angles repeat after 360 degrees (or 2 pi radians), so x and y stay within a definite range as a increases infinitely. The easiest way to think about it in this case is if you use the given equation for the x position of an object and you were to use that same equation with cos() replacing sin() for the y position of the same object, the object would move in a circle. When you only use it for x or y the object moves in a line on the axis with varying incremental movement (as it approaches the middle it is moving faster than at either end because the points would be closer together at either end of the circle)

A simple breakdown of how each number in that equations works:

x=c+r*sin(a)

  • c is the ā€œstarting pointā€ on the given axis youā€™re using (in this case 50)
  • r is the distance it will go from the starting point (so in this case it will cycle between 50-40=10 and 50+40=90) [represented by r because it would be the radius of the circle if you were using both x and y motion]
  • a will increase the rate of the cycles (#DWE# *2 cycle through its range twice as fast as #DWE#) [and is represented as a because it is being interpreted as an angle]

sin() calculates using radians, not degrees, so a way to make the calculations simpler is to throw a pi in the multiplier inside the sin(). so if I make the multiplier 2*pi instead of just 2, I know, without needing a calculator,that when #DWE# is 0, .5, 1, 1.5, 2, etc the object will be at the middle position (50) and when #DWE# is .25, 1.25, 2.25, 3.25, etc the object will be at the high extreme (90) and when #DWE# is .75, 1.75, 2.75, etc it will be at the low extreme (10)

3

Wow, I just looked at the animation they have to explain the breathing effect and it is CONFUSING! What they did was they had two circles, one with the given equation for the radius, with the opacity set to 50, and another with a radius set to 50, with the transparency equation they give [ ((sin(#DWE#*2)*60)+50) ] set as the opacity. Took me a second to interpret that properly, and since my explanation mainly focused on objects moving on an axis let me know if I can try to clarify any part of it in a more useful way.

4

Well thank you so much for replying. It may be because itā€™s 3am but itā€™s hard for me to wrap my head around this still. Iā€™ll read it again tomorrow haha. Iā€™m not really worried about the transparency in this case. Iā€™m mostly focused on the x and y axis so I just need to spend a but of time re-reading your explanation and I should be ok. Iā€™m trying to make a png file grow and shrink repeatedly as opposed to the interpAccel where it stops after so long. Thanks again and if I have more questions Iā€™ll ask tomorrow.

5

Hi @syntaxracing, Hi @shannon1callahan you inspired me to write a new micro tutorial as a simplified expansion of this discussion. :wink:

2 Likes
6

I didnā€™t want to crowd the tutorial you made, but I thought maybe you could help clarify this info for people:

Just for a comparison I threw together this equation that has a linear waveform that might also be helpful if someone wants the motion to be constant

(160 + ( 120 * ( sin ( #DWE# * 2 * pi ) ) ) )
vs
$ (round( floor( 2 * #DWE#+.5 ) / 2 )) = (floor( (2 * #DWE#+.5 ) / 2 )) ? 160 + 120 * (-1 + 2 * ( ( 2 * #DWE#+.5 ) - (floor( 2 * #DWE#+.5 )) ) ) : 160 - 120 * (-1 + 2 * ( ( 2 * #DWE#+.5 ) - (floor( 2 * #DWE#+.5 )) ) ) $

Waveform comparison:

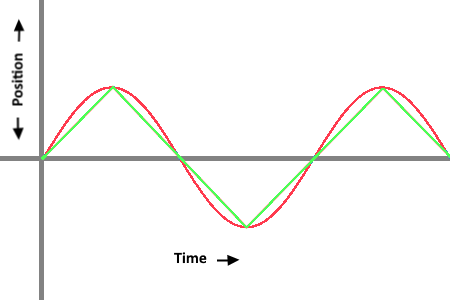
Movement comparison:

2 Likes
7

Hi @shannon1callahan, nice example! I am happy if somebody improves my tutorial :wink: Please feel free to add your valuable information whenever you like - it will be easier for designers to find it. :+1:

2 Likes