I was inspired by mechanical 7-segment digital watches, such as the example below:

At first glance it seems doable, but once I got going, I encountered a few challenges:
- At a certain point in time, a segment needs to “flip”, how to calculate that?
- It also requires a tag that increases in small units, such as
#Dsm# - And it requires this tag to start at 0 when the “flip” is to happen
- There is no smooth increase of an hour tag. #DWFHS# only increase by 0.25, that is not good enough.
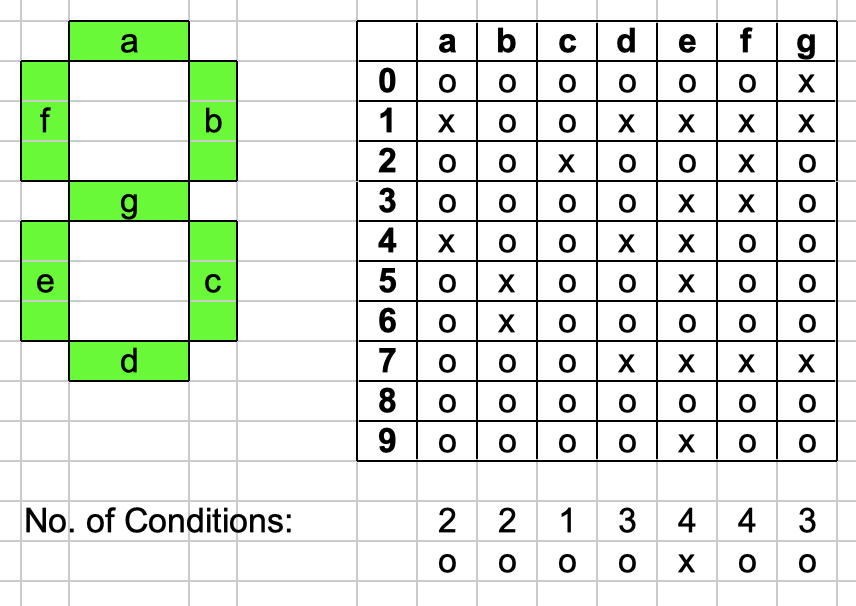
In the digital world, the 7-segments are defined from a to g. The following matrix shows when the segment should be on or off for the numbers 0-9, giving a number of conditions to work with:
So for simple watch face with 7-segments, without any movement or flip, those conditions can be defined as follows and can be used in the opacity field:
a:
$(#Ds#%10)=1||(#Ds#%10)=4?0:100$
b:
$(#Ds#%10)=5||(#Ds#%10)=6?0:100$
c:
$(#Ds#%10)=2?0:100$
d:
$(#Ds#%10)=0?100:$$(#Ds#%10)=1?0:$$(#Ds#%10)=2?100:$$(#Ds#%10)=3?100:$$(#Ds#%10)=4?0:$$(#Ds#%10)=5?100:$$(#Ds#%10)=6?100:$$(#Ds#%10)=7?0:$$(#Ds#%10)=8?100:$$(#Ds#%10)=9?100:$
e:
$(#Ds#%10)=0?100:$$(#Ds#%10)=1?0:$$(#Ds#%10)=2?100:$$(#Ds#%10)=3?0:$$(#Ds#%10)=4?0:$$(#Ds#%10)=5?0:$$(#Ds#%10)=6?100:$$(#Ds#%10)=7?0:$$(#Ds#%10)=8?100:$$(#Ds#%10)=9?0:$
f:
$(#Ds#%10)=0?100:$$(#Ds#%10)=1?0:$$(#Ds#%10)=2?0:$$(#Ds#%10)=3?0:$$(#Ds#%10)=4?100:$$(#Ds#%10)=5?100:$$(#Ds#%10)=6?100:$$(#Ds#%10)=7?0:$$(#Ds#%10)=8?100:$$(#Ds#%10)=9?100:$
g:
$(#Ds#%10)=0?0:$$(#Ds#%10)=1?0:$$(#Ds#%10)=2?100:$$(#Ds#%10)=3?100:$$(#Ds#%10)=4?100:$$(#Ds#%10)=5?100:$$(#Ds#%10)=6?100:$$(#Ds#%10)=7?0:$$(#Ds#%10)=8?100:$$(#Ds#%10)=9?100:$
Now to add movement or simulate the flip of a segment.
To simulate the movement/flip of a segment, I chose to change the width of the segment, depending on the conditions above. So to switch a segment “on”, that would be from width 0 to its maximum width. And “off”, the other way around. Through experimenting, I found a good value for the speed to change the width to be twice the width.
Example: For the watch face, further below, I used a segment which has the width 9. So the speed for changing the width is: (#DWFSS#/6)*18
(as some of you may know #Dsm#*18, will not work currently)
To limit the width change from 0 to 9, the clamp function can be used.
Since the time needs to start at 0 when changing the width, the calculation I use, for example last digit of the seconds, is:
"smooth value" - "exact value": (((#DWFSS#/6)%60)-#Ds#)*18
So the whole width increasing formula is:
(clamp(((((#DWFSS#/6)%60)-#Ds#)*18),0,9))
And decreasing is the same as above but starting at width 9:
(clamp((9-(((#DWFSS#/6)%60)-#Ds#)*18),0,9))
Next, it requires the exact time at which the width is to be changed. This is where the conditions come into play. Since these conditions are way to nested, I decided to split things up into 3 parts:
- Action to decrease the width
- Action to increase the width
- Time at which the segment is “on”. I noted that the flip takes a bit time, so only for the last digit of the seconds, I added a 0.5 delay.
Example, last digit of the seconds:
Segment a action off :
$(#Ds#%10)=1||(#Ds#%10)=4?(clamp((9-(((#DWFSS#/6)%60)-#Ds#)*18),0,9)):0$
Segment a action on:
$(#Ds#%10)=2?(clamp(((((#DWFSS#/6)%60)-#Ds#)*18),0,9)):$$(#Ds#%10)=5?(clamp(((((#DWFSS#/6)%60)-#Ds#)*18),0,9)):$
3x Segment a ON (width is 9 when):
$((#DWFSS#/6)%10)>=0&&((#DWFSS#/6)%10)<1?9:0$
$((#DWFSS#/6)%10)>2.5&&((#DWFSS#/6)%10)<4?9:0$
$((#DWFSS#/6)%10)>5.5?9:0$
These 3 parts are defined for each segment of each of digit of digital time format HH:MM:SS. You can imagine that this requires quite a number of elements.
These are the formulas//conditions for each digit when something is to happen:
Last digit of SS: #Ds#%10
1st digit of SS: #Ds#/10
Last digit of MM: (#DWFMS#/6)%10
1st digit of MM: (#DWFMS#/6)/10
Lsat digit of HH: #Db#%10
1st digit of HH: floor(Db#/10)
You may think why #Db#, that is not a smooth value. I mentioned earlier, that the smooth rotation to the hour is not good enough. I found the following formula to be useful for that, using 2 conditions when to change the width:
$floor(#Db#/10)=1&&#DWFMS#/6=0?(clamp((9-(((#DWFSS#/6)%60)-#Ds#)*18),0,9)):0$
Which means:
So when the 1st digit of the hour is “1” and the minute has turned to exactly “0”, then change the width.
What else?
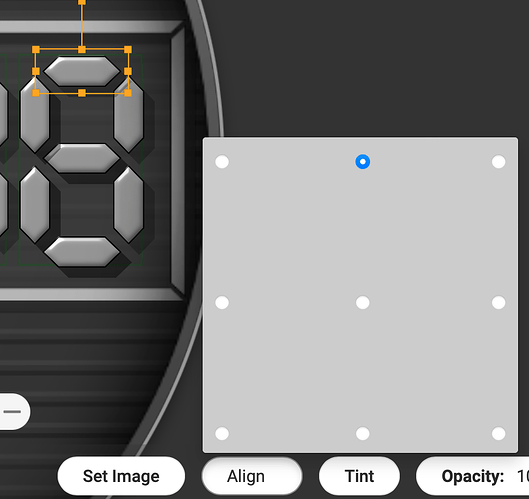
To simulate the flip, each segment, depending where it sits, needs to have the correct alignment:
- Segment a needs to be aligned top center
- Segments b and c need to be aligned center right
- Segment d needs to be aligned bottom center
- Segment e and f need to be aligned middle left
- Segment g need s to be aligned middle top (well up to you really…)
Example:
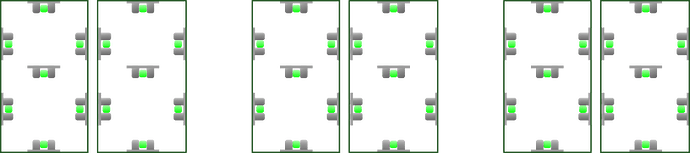
RESULT:
This result of putting all of the above together for each single segment.