[Tutorial] Elliptical Motion

Resources Expressions
1

I’ve been trying to create a formula to have 3 dots move on each of the following 3 paths:

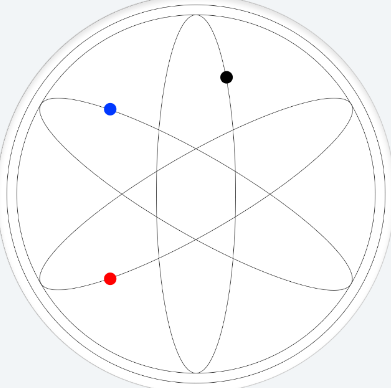
First off, I want to thank @Mellin for his great tutorial about circular motion as it gave me a place to start!

Now on to the actual tutorial.

For the black dot, it’s not that hard. You’ll use something like this (based entirely on Mellin’s explanations which explain what all the elements in the below formulas are):
x: ((33*(sin((#DWFMS#/180)pi)))+160)
y: ((140(cos((#DWFMS#/180)*pi)))+160)

For the next 2 paths it gets a bit tricky. Here’s a bit of background.

How is an ellipse defined?

x: asin(t)
y: bcos(t)

In the above example, a=33 (the “width” of the ellipse), b=140 (the “heigth” of the ellipse) and t=(#DWFMS#/180)*pi (the angle, measured in Radians).

How do you rotate an ellipse?

Intuitively, you might say that you could use something like this:
x: asin(t + u)
y: bcos(t + u)
where u=the angle to rotate the ellipse by.

Unfortunately, it’s not that easy and the above formula would give you basically the same motion as the original one. In order to rotate the ellipse, you actually have to rotate your system of coordinates!

So, if x and y are your original coordinates, x’ and y’ after rotating the coordinate system by an angle “u” would be the following:
x’ = xcos(u) - ysin(u)
y’ = xsin(u) + ycos(u)

Replacing the x and y from the “original” ellipse formula, you get this:
x’ = acos(t) cos(u) - bsin(t)sin(u)
y’ = acos(t) sin(u) + b*sin(t)*cos(u)

Back to our example

The blue dot
By replacing our values for a, b and t from the black dot and determining the wanted “u” angle (I know it’s 30 degrees), we get the following formula:
x: ((140cos((#DWFM#/180) pi)* cos(pi/6)-33sin((#DWFM#/180) pi)sin(pi/6))+160)
y: ((140cos((#DWFM#/180)* pi)* sin(pi/6)+33sin((#DWFM#/180) pi)*cos(pi/6))+160)

The red dot
This is similar with the blue dot just that my angle is 150 degrees (or -30 degrees) and as such, I use 5pi/6 for “u”:
x: (((140cos(-(#DWFM#/180)* pi)* cos(5pi/6))-(33sin((#DWFM#/180)* pi)sin(5pi/6)))+160)
y: (((140cos(-(#DWFM#/180) pi)* sin(5pi/6))+(33sin((#DWFM#/180)* pi)cos(5pi/6)))+160)

I also changed the direction of the movement by using a “-” sign.

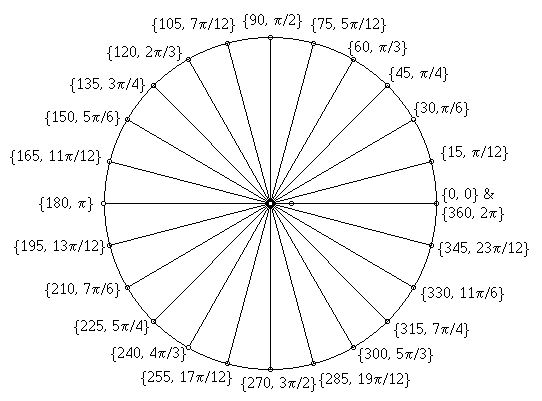
Angles to Radians (how do I get “u”)

The sin and cos formulas actually work with Radians, not Degrees. In order to convert Degrees to Radians you have to consider that 2*pi radians equals 360 degrees. This means that 1 radian = 180/pi degrees, and 1 degree = pi/180 radians. You can also use the image below for some “common” angles.

Conclusion

I hope you find this useful and that you’ll come up with some awesome designs! Can’t wait to see them! Also, if there’s any feedback to this tutorial, don’t hesitate to leave a comment.

Enjoy,
Mircea

6 Likes
2

Or using sin(rad(x)), to make formulae much simpler:

black dot: (delayed phase by 30°, to not collide)

x, y:

(220+(sin(rad(#DWFSS#*2-30))*14))

(220+(cos(rad(#DWFSS#*2-30))*42))

blue dot: 30°

x' =x*cos(rad(u))-y*sin(rad(u))

y' =x*sin(rad(u))+y*cos(rad(u))


x' =cos(rad(t))*cos(rad(u))*a-sin(rad(t))*sin(rad(u))*b

y' =cos(rad(t))*sin(rad(u))*a+sin(rad(t))*cos(rad(u))*b

x, y:

(220+cos(rad(#DWFSS#*2))*cos(rad(30))*42-sin(rad(#DWFSS#*2))*sin(rad(30))*14)

(220+cos(rad(#DWFSS#*2))*sin(rad(30))*42+sin(rad(#DWFSS#*2))*cos(rad(30))*14)

red dot: 150° (or -30°)

x, y:

(220+cos(rad(#DWFSS#*2))*cos(rad(150))*42-sin(rad(#DWFSS#*2))*sin(rad(150))*14)

(220+cos(rad(#DWFSS#*2))*sin(rad(150))*42+sin(rad(#DWFSS#*2))*cos(rad(150))*14)

4 Likes
3

To take this a step further, I’ve made an elliptical face, as a circle would appear if seen at a slant. On this face, the numbers wouldn’t be evenly spaced by degrees, they’d be “squashed” in around the edges. Likewise, the hand wouldn’t move by the regular degrees.

The blue dot moves up and down the y-axis of the inner, white circle as a cos to the angle. The green dot moves side to side the x-axis of the larger grey circle. The red dot moves with both these coordinates.
As you can see, the angle of the red dot does not follow the angle of the second hand. To find this angle I took asin to the x-pos of the red dot (or green dot), divided by the distance to the red dot.

Just if anyone wants to have a 3d feel to the elliptical watch face.

1 Like
6

Very nicely done @msm030 !
There are some sin/cos values that can be of interest, using Pythagoras and the fact that they relate to a circle with a radius of 1.
For a given angle, (cos(a))^2 + (sin(a))^2 = 1
for π/4, 45°, cos(π/4) = sin(π/4) = sqrt(2)/2
for π/6, 30°, sin(π/6) = 0.5 so cos(π/6) = sqrt(1-0.25) = sqrt(3)/2
Same goes with π/3, just the other way around sin(π/3) = sqrt(3)/2
Interestingly, cos(2π/5) (or 72°, the angle in a pentagon) is half the Golden Ratio R = 2/(1+sqrt(5)).
Can’t remember the reason for this, but it was a very clever one.

1 Like
7

I use the same formula for the “moon” effect of the second’s planet:

4 Likes