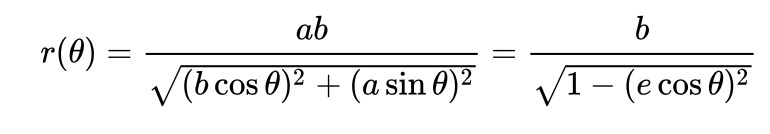Looks good to me, but the Hands don’t seem to be at the correct angle for the oval 
1 Like
So if I understand you correctly, you mean that the first blue hour hand (pointing at 1 o’clock, as in a circle) does not appear to be right in a oval face. That is what I am also saying. I think it should be approximately there where the first back line is after 12 o’clock. Those black lines or now only based on my guessing where they could be. By reference of the presumed reality. In the end, that is a kind of final validation for everything we simulate.
So if that’s still correct, because of the oval, the normal hour hand and it’s formula (#DWFKS#) won’t work in a oval face. Then thus is necessary an adjustment of this formula. I assume the reduction on the y axis must have an influence on that formula, but I am still guessing. That bothers me. 
1 Like
I made a test to see what the error is . Just a Dial foreshortened on the Y axis . One of the Maths Geniuses will join in . It will be about a combination of Sin Cos and Tan . There will be
someone who can do it with Pythagerous .
.
.
4 Likes
Angle is the simplest. Solution is in tangens and acrus tangens.
For lenght is little more complicated
2 Likes
Ha Ha . For me Knowing that and Doing that are two different things . I must have a Look at the Sundial Faces . See If I can find an Inspectable . I think there is one on my Bits Box Collection .
2 Likes
Hi. Can you share the formula for the evolving angle of for example the hour hand. I assumed that the reduction on the y axis, has influence on the sinus evolution and thus on the tangent value. But what is the correct formula for the hour hand in a oval form (elliptic) when the y axis is reduced with 50%? Thanks.
2 Likes
I started this in another topic, but it belongs here.
I will first try to provide some hints, sketches and basic formulas to point you to deduct and derive the right formulas your self.
Lets start with this:
Right triangle - Wikipedia
In our case important are these principal properties of right triangle like
- sum of its internal angles is always 180°
We can name our angles and sides like this
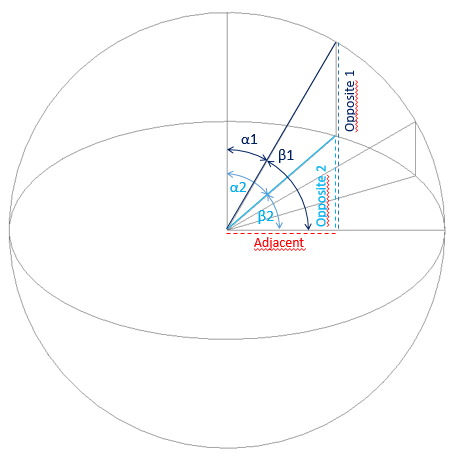
Facer rotates elements by angles given in degrees, but calculates functions with angles in radians, which means we need to convert the angle used in trigonometric functions like for example #DWFHS#*3,14/180 and the resulting angle back to degrees like atan(xy)*180/3,14
There was request to have the oval of 1/2 height of the regular circle, so there will be fixed ratio Opposite2=opposite1/2
now go substitute…
tan(β2)=opp2/adj=(opp1/2)/adj=(opp1/adj)/2=(tan(β1))/2
β2=atan((tan(β1))/2) and so forth
5 Likes
OK. here it goes… (open for inspection)
So what’s the math in this example?
I took an ellipse which has a width twice that of its height, so 100:50.
the radius an ellipse is defined by the equation:
where by “e”, is the relation ship between the height and width:
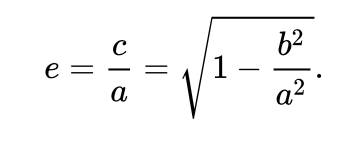
so that should equate to 0.866 using 100 and 50.
Putting all that into a formula for a rotating hand, not forgetting degrees to radiant conversion, then the length of the hand should be:
(100/(sqrt(1-0.866*cos(rad(#DWFSS#)))))
But, the formula is only good for 180°. And my drawing of ellipse is probably not exact, and not sure if the Facer math is accurate. Anyway, I used 2 pairs of hands (using sinus in the formula) and 3 lines (images, using cosine). The Arrow hand also changes width with the same formula. And I needed to adjust “e”.
In my sample, you’ll also find 2 rectangles (standard Facer elements) which also kind of work.
But maybe I got it wrong somewhere, but kind of works for me 
6 Likes
Maravilhoso!!!
4 Likes
Hi
Thanks for your introduction.
I understand the need to reconvert back to degrees. I noticed there are 2 arguments x and y used in that part of the text. Do you mean atan2 and does Facer support atan2, in the documentation i found only atan with 1 argument. And has this an effect somehow on the substitution.
Thanks
1 Like
sorry for confusion, I have written those paragraphs in different times.
I meant xy like “whatever” single argument for the atan function when goes about units.
Then later I refer to the angles like on the sketch with greek letters and to the argument like ratio between opposite and adjacent sides of compared triangles.
3 Likes
I was impatient, so I did not play with the shadow lenght, just cheated a bit with “mask”.
6 Likes
Haha . Brilliant . If you can do the Angle you can do the Length . 
5 Likes
Awesome, this Topic is definitely getting Bookmarked thanks everyone 
5 Likes
Cool! And maybe no shadow during the night … 
4 Likes
I will change the sun icon to light bulb icon for that time
5 Likes
Super watch and contribution, Peter and Tom. Did you notice how much an oval form can offer in terms of creativity, looks, depth, liberating space for other elements. Not to forget stunning animations and still be entertaining, informative. I feel digital faces offer here so much more opportunities. I surely will apply these experiences on other opportunities. I promote the oval as the form of 2023. I suspect many will follow.
6 Likes
…não sei como descrever… 
2 Likes
Oval is good- digits 1 - 23 a bit simple for my taste. There nothing like a good tourbillon and gearwheels to exercise the brain - applying that to an oval, now that’s a challenge!
3 Likes
So, i made another oval face. This time with oval hands for hour minutes and seconds. Including oval functioning objects. My goal is reached, it seems. Any one else did oval faces?
Greetings
Patrick
3 Likes