[Mini-Tutorial] InterpAccel - Fly In Motion

Watchface Design Expression Help
1

Hello all,

Just wanted to elaborate on a previous post for the InterAccel function found HERE.

I had some remaining questions from the documentation provided. I think I have these all worked out now and you can see below how the function can be used.

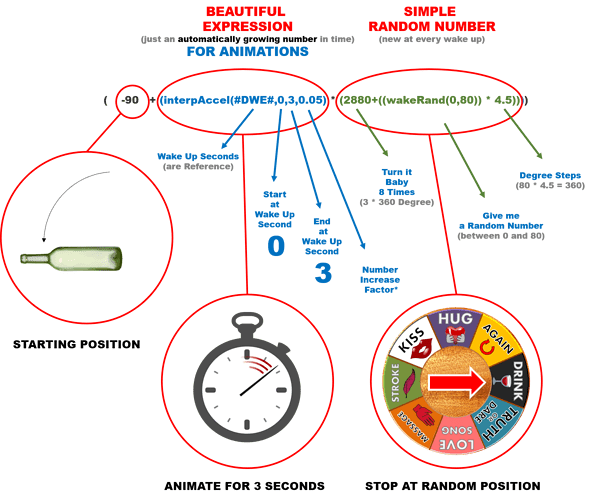
Here is a breakdown of the expression and its elements:

interpAccel(Time format, Min, Max, Acceleration Factor)

Time Format = this can be any time related tag. Generally #DWE# is easiest to start with since it is a simple running time that starts when you wake your watch.
Min = Start point in the Time Format you chose above
Max = End point in the Time Format you chose above
Acceleration Factor = Speed at which the interval accelerates

From this I had a few questions in trying to implement this expression. The difficulty is understanding that you need to have a start and end point. This is different from the expression above. The full formula is really:
(x+(interpAccel(Time format, Min, Max, Acceleration Factor)*y))

x = starting point
y = end point

For instance, here are three variables on an element that you can use:

Position (i.e. x and y axis)
Placing this expression in the x axis will move an element

  • Animation will begin at ‘0’ seconds of #DWE# (wake)
  • Element moves from x-axis position of 0 to 160
  • Animation will end at position 160 over the course of 2 seconds
    (0+(interpAccel(#DWE#, 0, 2, 1.5)*160))

Rotation
@Tomas has a great tutorial on this example posted HERE:

  • Animation will begin at ‘0.2’ seconds of #DWE# (wake)
  • element from position 0 to #DWFSS# (i.e. current seconds position)
  • Animation will end at position #DWFSS# over the course of 0.6 seconds
    (interpAccel (#DWE#,0,2,0.8) * #DWFSS#))

Size
Placing this expression in the Size variable (Height, Width, Radius) will increase/decrease its size:

  • Animation will begin at ‘4’ seconds of #DWE# (wake)
  • Element will start at size 0
  • Size will increase to 8 over the course of 2 seconds
    (0+(interpAccel(#DWE#, 4, 6, 2)*8))

The last mysterious piece of the expression is the acceleration factor. My best guess to how this works is in the diagram below:

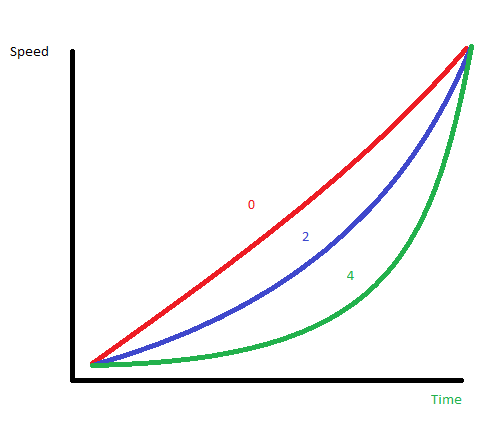
Decreasing the number to 0 will smooth the animation. Increasing it appears to give a ‘ramp up’ in the observed animation.

A few more example faces:

7 Likes
2

I was banging my head on this expressions, because of lack of official documentation (:triumph:).
Thank you SO MUCH, @eradicator09!! Great explanation :+1:

Paolo

1 Like
3

I think this simple picture could be also heplpful for designers using this function for the first time:

xxxxBild1.png1839×1500 571 KB

Here would be the link to the watch face, I used as an example :wink:

3 Likes
4

Great tutorial again. I read through the posts the other day about this, and this provides even more clarity :+1:

1 Like
5

Just wanted to add this to clarify the starting point and end point. The start point is the true x or y coordinate. The end point is technically a calculation of the distance between where you start and where you want to end.

For instance if you start at 160 and want to get to 180, then the function would look like this:

(160+(interpAccel(#DWE#, 0, 2, 1.5)*20))

160 + 20 = 180

For reverses in motion, i.e. from point 160 to 40

(160+(interpAccel(#DWE#, 0, 2, 1.5)*-120))

160 - 120 = 40

In the rotation example above from @Tomas the starting point is 0 since there is no prefix to the expression.

4 Likes